En matemática, las funciones trigonométricas son las funciones determinadas con el objetivo de extender la definición de las razones trigonométricas a todos los números reales y complejos. Estas usualmente incluyen términos que describen la medición de ángulos y triángulos, tal como seno, coseno, tangente, cotangente, secante y cosecante.
Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras de muchas aplicaciones.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones
Seno
El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).
Su abreviatura son sen o sin (del latín sinus).
Coseno
El coseno de un ángulo α se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).
Su abreviatura es cos (del latín cosinus).
Tangente
La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).
Su abreviatura son tan o tg.
Cosecante
La cosecante es la razón trigonométrica recíproca del seno, es decir csc α · sen α=1.
La cosecante del ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).
Su abreviatura es csc o cosec.
Secante
La secante es la razón trigonométrica recíproca del coseno, es decir sec α · cos α=1.
La secante de un ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto contiguo o cateto adyacente (b).
Su abreviatura es sec.
Cotangente
La cotangente es la razón trigonométrica recíproca de la tangente, por lo tanto tan α · cot α=1.
La cotangente de un ángulo α de un triángulo rectángulo se define como la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a).
Su abreviatura es cot, cotg o cotan.
Ejercicios:
Calcular el valor de x de cada figura utilizando las razones trigonométricas viastas:
Figura 1:
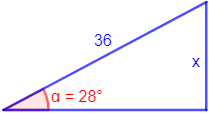
Conocemos la hipotenusa y el ángulo. Como queremos calcular el lado opuesto, utilizamos el seno:
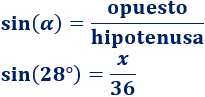
Figura 2:
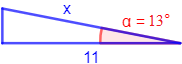
En esta figura conocemos el lado adyacente y el ángulo. Para calcular la hipotenusa, utilizamos el coseno:
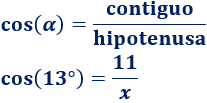
Figura 3:
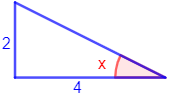
Como conocemos el lado opuesto y el adyacente al ángulo, utilizamos la tangente:
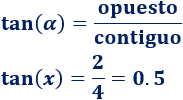

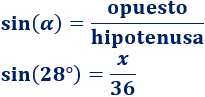

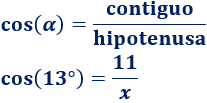

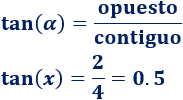







No hay comentarios:
Publicar un comentario