1- Radianes
Un radián es la unidad de medida de un ángulo con vértice en el centro de una circunferencia y cuyos lados delimitan un arco de circunferencia que tiene la misma longitud que el radio. El radián (rad) es la unidad de medida para ángulos en el Sistema Internacional de Unidades (S.I.).
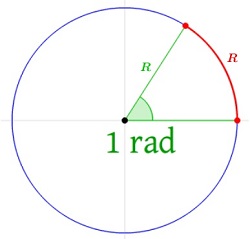
La relación del radián con la otra unidad de medida para ángulos más ampliamente utilizada, los grados sexagesimales o simplemente grados (º), es la siguiente:
1 vuelta completa de la circunferencia = 360º = 2 · π radianes
Para entender la anterior igualdad, se parte de saber que la medida en radianes de un ángulo (θ) medido en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia, es decir:
| Longitud del arco |
|
θ(radianes) = |
| |
| Radio |
|
Por tanto, cuando se trata del ángulo correspondiente a una circunferencia completa, cuya longitud total es 2·π·r (siendo r el radio de la circunferencia) le corresponden en radianes un ángulo de:
| 2·π·r |
|
θ(circunferencia completa) = | = 2·π radianes | |
| r |
|
En el sistema sexagesimal, el ángulo que abarca la circunferencia completa mide 360º, por lo que se puede establecer la ya vista relación entre grados y radianes:
1 vuelta completa = 360º = 2 · π radianes
Otras equivalencias útiles entre grados y radianes son las siguientes:
0º = 0 rad
90º = π/2 rad
180º = π rad
2- Sistema sexagesimal
El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad fundamentalmente para la medida de ángulos y también en la medida del tiempo.
La unidad de medida de ángulos en el sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales, o bien un ángulo recto en 90 partes, o un ángulo completo en 360 partes. A cada una de esas partes se les llama grado (º). Así, un ángulo llano mide 180º, un ángulo recto 90º y un ángulo completo 360º.A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos.
Medidas de ángulos: 1 grado (º) → 60 minutos (´) → 60 segundos (´´)
• Medidas de tiempo: 1 hora → 60 minutos (´) → 60 segundos (´´)
Ejemplo: 38º 50´ 35´´ (38 grados, 50 minutos y 35 segundos). Si se omiten los minutos y segundos, por ejemplo, 45º, es porque se entiende que es 45º 0´ 0´´.
32º → medida simple
11´´ → medida simple
52º 17´ 45´´ → medida compleja
4º 22´ → medida compleja
Para sumar grados expresados en medidas complejas, primero se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos, y se suman, como se indica en el siguiente ejemplo de la figura:
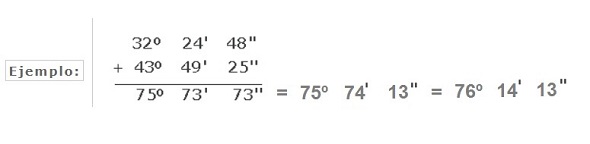
Como se ve en el ejemplo anterior, si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos. Se hace lo mismo para los minutos, si estos resultasen también una cantidad mayor de 60.
Ejercicios:
Pasa a grados los siguientes radianes:
![]()
![]() radianes a grados sexagesimales
radianes a grados sexagesimales![]()
![]() radianes a grados centesimales
radianes a grados centesimales
Sabemos que ![]() radianes son 180 grados.
radianes son 180 grados.
![]()
 grados sexagesimales
grados sexagesimales![]()
 grados sexagesimales
grados sexagesimales
Pasa de grados a radianes las siguientes cantidades:
![]()
![]()
![]()
![]()
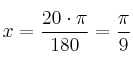 radianes
radianes
 radianes
radianes
No hay comentarios:
Publicar un comentario