El teorema de Tales es una ley de la geometría que nos indica que si se traza una línea paralela a cualquiera de los lados de un triángulo tendremos como resultado un triángulo semejante el triángulo original.
Dicho de otro modo, si cortamos un triángulo dibujando una recta paralela a uno de sus lados, obtendremos un triángulo semejante al previamente existente.
Dos triángulos son semejantes cuando sus ángulos correspondientes son congruentes (miden lo mismo) y sus lados homólogos son proporcionales entre sí.
Para entenderlo mejor, observemos la siguiente figura:

Por el teorema de Tales se puede concluir que α=δ y β=ε
Además, como mencionamos previamente, los lados son proporcionales, por lo que se cumple que:

Para entender el Teorema de Tales es necesario entender la razón entre dos segmentos.
Por ejemplo, tenemos estos dos segmentos:

Al segmento rojo, que empieza en el extremo A y termina en el extremo B, se le llama segmento AB.
Si dos segmentos tienen alguna relación entre ellos, se utilizan las mismas letras para nombrarlos, pero como no pueden repetirse, se utiliza la comilla simple al lado de cada letra y esa comilla se lee prima.
Por tanto A’, se leería "A prima".
Así pues, al segmento azul, que empieza en A’ y termina en B’, lo llamaremos segmento A’B’.
Si el segmento AB mide 5 cm y el segmento A’B’ mide 10 cm, ¿Cuál es la razón de estos dos segmentos?
Sólo tenemos que dividir la longitud del segmento AB entre la longitud del segmento A’B’:

La razón de esos dos segmentos es 0,5, que significa que AB es la mitad que A’B’.
También podemos calcular la razón dividiendo la longitud del segmento A’B’ entre la longitud del segmento AB:

En este caso, la razón es 2, o con otras palabras, el segmento A’B’ es el doble que el segmento AB.
Decir que el segmento AB es la mitad que el segmento A’B’, es lo mismo que decir que el segmento A’B’ es el doble que el segmento AB.
Ejercicios
1. ¿Cuánto mide el segmento x en este dibujo?
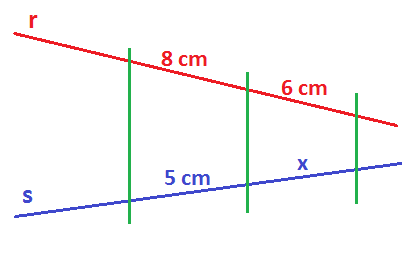
Sabemos lo que miden los dos segmentos de r, pero falta por saber cuánto mide uno de los segmentos de s, por lo que a ese segmento le llamamos x.
Entonces, según el teorema de Tales, los tramos que están enfrentados tienen la misma razón, por lo que sus divisiones deben de dar lo mismo y por tanto las podemos igualar:

Se despeja la x.

Ahora, el 8 que está multiplicando a la x, pasa al segundo miembro dividiendo:

Y finalmente operamos para calcular el valor de x:

Que si lo compruebas, los pares de segmentos serán proporcionales
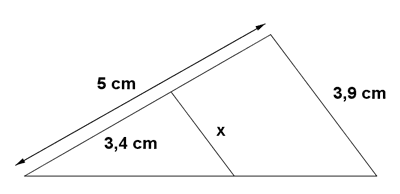
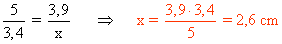
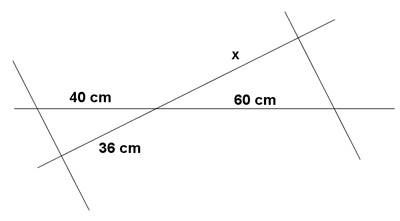
Los dos triángulos son semejantes, por lo tanto, sus lados son proporcionales:
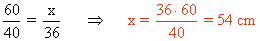
No hay comentarios:
Publicar un comentario